Piezoelectricity¶

This module introduces the fundamentals of piezoelectricity.

Related material:

Alfonso Rodriguez-Molares <alfonso.r.molares@ntnu.no>

Stefano Fiorentini <stefano.fiorentini@ntnu.no>

Last edit 17-09-21

Introduction¶

The piezoelectric effect was first described on a scientific publication in 1880 by the Curie brothers, who discovered that some crystals, such as quartz, showed an electrical charge when they were subjected to a mechanical stress.

A few years later, Lippmann predicted the existence of the converse piezoelectric effect, i.e. that piezoelectric materials subjected to an electric field should undergo a mechanical deformation. Shortly after Lippmann’s prediction, the Curie brothers confirmed the converse piezolectric effect experimentally.

Piezoelectricity can be defined as the conversion of electrical energy into mechanical energy, and viceversa.

Piezoelectric stress constant \(g\)¶

We are going to replicate the Curie brothers’ result. We have a slab of a piezoelectric material (PZ27), with dimensions x = 40 mm, y = 40 mm, z = 2 mm. We subject the slab to a mechanical stress by applying a force on the electrodes and we measure the voltage difference, as depicted in the figure below.

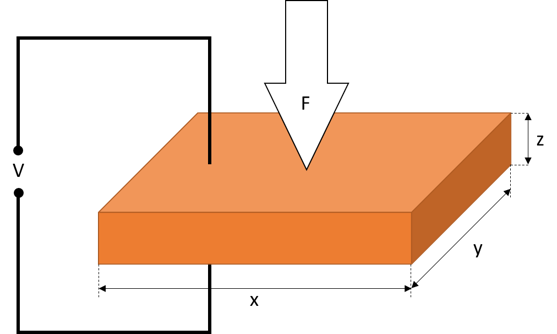
The piezoelectric stress constant \(g\), which is measured in (m ²/C), describes the electric field \(E\) in (V/m) that is generated when we subject the material to a stress \(T\) (N/m ²)

\[E = g T\]

We apply a force of 100 Newtons on top of the slab and we measure a voltage between the electrodes of 3.3375 V.

Compute the piezoelectric stress constant

% g = E/T
%
% where E = V/z, and T = F/x/y, thus

x = 40e-3;  % x dimension in [m]
y = 40e-3;  % y dimension in [m]
z = 2e-3;   % z dimension in [m]
F = 100;    % Applied force in [N]
V = 3.3375; % sensed voltage in [V]

g = V * x * y / z / F;

fprintf(1, 'Piezoelectric voltage constant g = %.2f m^2/C\n', g)

Exercise: A student weighs 95 kgs and steps on a slab of PZ27 piezoelectric ceramic. The slab has an area of 0.09 m ² and a thickness of 2 cm. The student measures the voltage of the slab using a voltmeter.

What is the measured voltage after the student steps on the slab?

Piezoelectric strain constant \(d\)¶

We are going to study the converse piezolectric effect. We have the same slab as before but now we apply a voltage difference at the electrodes and we measure how much the materials deforms, as depicted in the figure below

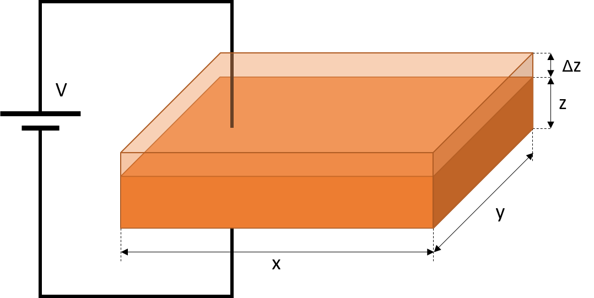
The piezoelectric strain constant \(d\), which is measured in (m/V), defines the strain (m/m) that occurs when the material is subjected to an electric field \(E\) in (V/m)

\[ \begin{align}\begin{aligned} \Delta z = d V\\\Delta z / z = d / z\\\epsilon = d E\end{aligned}\end{align} \]

We apply 100 Volts between electrodes and we observe that the material expands by 42.5 nanometers

Compute the piezoelectric strain constant

% d = S/E
%
% where E = V/z, and S = Deltaz/z, thus

V = 100;            % applied voltage [V]
Deltaz= 42.5e-9;    % measured deformation [m]

d = Deltaz/V;
fprintf(1, 'Piezoelectric strain constant d = %.2f m/V\n',d)

Relation between \(d\) and \(g\)¶

The two piezolectric constants are related by

\[d = \epsilon g\]

where \(\epsilon\) is the electric permittivity of the material (F/m). The permittivity measures the amount of charge produced in a dielectric material when it is exposed to an electric field.

Check the difference between absolute and relative permittivity and compute the relative permittivity of the material

epsilon = d/g;
fprintf(1, 'Relative permittivity E_r = %.2f\n', epsilon)

Piezoelectric coupling coefficient \(k\)¶

The piezoelectric coupling coefficient \(k\) represents the ability of the material to transform electrical energy to mechanical energy and viceversa. This transformation of energy is used both in sensors and actuators, and it is the most important parameter to determine efficiency of the material.

The coupling coefficient can be computed as

\[k = \sqrt(g d Y)\]

where \(Y\) is the Young modulus of the material, defined in in (N/m ²). We know that the material has a Young Modulus of 43 GPa.

Compute the coupling coefficient

Y = 43e9;           % Young modulus [Pa]
k = sqrt(g*d*Y);
fprintf(1, 'Coupling coefficient k = %0.2f\n', k)