Physics - Points, points, point everywhere
This exercise reviews the basic relations in ultrasonic wave propagation and echo ranging, with points.
Related materials:
by Alfonso Rodriguez-Molares (alfonso.r.molares@ntnu.no) 17.07.2016
Contents
A point source
A point source is immersed in a fluid: an infinite, isotropic, and homogenous domain with unknown speed of sound. We know however that the fluid density  =1052 kg/m3 and that its bulk modulus
=1052 kg/m3 and that its bulk modulus 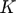 = 2.6196e9 Pascals.
= 2.6196e9 Pascals.
- Can you calculate the speed of sound
![$c_0~[\textmd{m/s}]$](exercise_points_eq08362350054553592623.png) in the fluid?
in the fluid?
rho=1052; % domain density [kg/m3] K=2.6196e9; % domain coefficient of stiffness [Pa] c0=sqrt(K/rho) % domain speed of sound [m/s]
c0 = 1.5780e+03
- The source emits a bandpass pulse centered at frequency
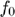 =10 MHz. What is the wavelength
=10 MHz. What is the wavelength ![$\lambda~[\textmd{m}]$](exercise_points_eq14910925191047345796.png) of the transmitted pulse?
of the transmitted pulse?
f=10e6; % central frequency [Hz] lambda=c0/f % wavelength [m]
lambda = 1.5780e-04
- What is the period of the transmitted pulse?
T=1/f % period [s]
T = 1.0000e-07
A point reflector
Let's consider the location of the source as the origin of coordinates and let us place a point reflector at 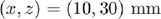 ,
,

x=10e-3; % x-position [m] z=30e-3; % z-position [m] % % create figure % figure1 = figure('Name','background','Color',[1 1 1]); % hold on; grid on; % plot(0,0,'ro','linewidth',2,'markersize',5); axis equal; % plot(x*1e3,z*1e3,'bo','linewidth',2,'markersize',5); % set(gca, 'ydir', 'reverse'); % box('on'); % xlabel('x [mm]'); % ylabel('z [mm]') % legend('Point source','Point reflector'); % title({'Point Source and Reflector'}); % set(figure1,'InvertHardcopy','off');
Notice in the previous figure that we refer to the ordinates as z-axis, not y-axis. Also you may notice that the z-axis is reversed (it increases as we get down). That is the common way we represent space in ultrasound imaging. You better get used to it!
- Can you calculate the 2-way time-of-flight (TOF)? note: the 2-way TOF is the amount of time that it takes for the transmitted pulse to reach the point scatterer and back to the source.
r=sqrt(x^2+z^2); % distance [m] TOF=2*r/c0 % time of flight [s]
TOF = 4.0079e-05
- We know the reflector is made of a material with density
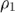 = 2028 kg/m3 and speed of sound
= 2028 kg/m3 and speed of sound 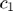 =3190 m/s. Can you calculate the pressure reflection coefficient
=3190 m/s. Can you calculate the pressure reflection coefficient 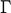 ?
?
rho1=2028; % particle's density [kg/m3] c1=3190; % particle's speed of sound [m/s] z1=rho1*c1; % particle's acoustic impedance [kg/m2/s] z0=rho*c0; % domain acoustic impedance [kg/m2/s] Gamma=(z1-z0)/(z1+z0) % Reflection coefficient [unitless]
Gamma =
0.5916
- The point reflector has suddenly moved and now the pulse arrives at TOF = 30e-6 s. Can you calculate the new position
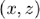 of the point reflector?
of the point reflector?
% Nope. The position $(x,z)$ of the point reflector can not be retrieved, but % we can calculate the distance the point reflector is located at: TOF=30e-6; % time of flight [s] r=TOF/2*c0 % distance [m]
r =
0.0237